Function
Measure time while Pin  remains in State; usually to measure the charge/discharge time of resistor/capacitor (RC) circuit.

• Pin  is any SX IO pin (RA.0 .. RA.7, RB.0 .. RB.7, RC.0 .. RC.7, RD.0 .. RD.7, RE.0 .. RE.7).
• State  is a constant (0 - 1) that specifies the desired state to measure. Once Pin is not in State, the command ends and stores the result in Variable.
• Variable  is a byte or word variable in which the time measurement will be stored. The unit of time for Variable is 2 microseconds multiplied by Resolution (if specified).
• Resolution  is an optional variable or constant (1 - 255) that specifies the units for Variable, in increments of 2 microseconds (default is 1 when not specified).

explanation
RCTIME can be used to measure the charge or discharge time of a resistor/capacitor circuit. This allows you to measure resistance or capacitance; use R or C sensors such as thermistors or capacitive humidity sensors or respond to user input through a potentiometer. In a broader sense, RCTIME can also serve as a fast, precise stopwatch for events of very short duration.

When RCTIME executes, it starts a counter. It stops this counter as soon as the specified pin is no longer in State (0 or 1). If pin is not in State when the instruction executes, RCTIME will return 0 in Variable. If pin remains in State longer than 255 timing cycles RCTIME returns 0.

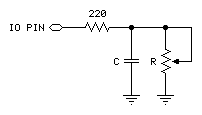
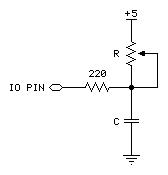
The figure below shows suitable RC circuits for use with RCTIME. Circuit A is preferred, because the SX TTL logic threshold is approximately 1.4 volts. This means that the voltage seen by the pin will start at 5V then fall to 1.4V (a span of 3.6V) before RCTIME stops. With Circuit B, the voltage will start at 0V and rise to 1.4V (spanning only 1.4V) before RCTIME stops (this could be changed by setting the Pin threshold to CMOS). For the same combination of R and C, Circuit A will yield a higher count, and therefore more resolution than Circuit B.

Here's a typical sequence of instructions for Circuit A, using a 0.1 µF capacitor and a 10 kΩ pot.

Start:
  TRIS_B = %00000000                            ' make LED pins outputs

Main:
  HIGH RA.0                                     ' charge the capacitor
  PAUSEUS 250                                   '   for 250 us
  RCTIME RA.0, 1, analog, 5                     ' measure in 10 us (2 x 5) units
  RB = analog
  PAUSE 100
  GOTO Main

Using RCTIME is very straightforward, except for one detail: For a given R and C, what value will RCTIME return? It's easy to figure, based on a value called the RC time constant, or tau (τ) for short. Tau represents the time required for a given RC combination to charge or discharge by 63 percent of the total change in voltage that they will undergo. More importantly, the value t is used in the generalized RC timing calculation. Tau's formula is just R multiplied by C:

τ = R x C

The general RC timing formula uses τ to tell us the time required for an RC circuit to change from one voltage to another:

time = -τ x ( ln(V_final / V_initial) )

In this formula ln is the natural logarithm; it's a key on most scientific calculators. Let's do some math. Assume we're interested in a 10 kΩ resistor and 0.1 µF capacitor. Calculate τ:

τ = (10 x 10³) x (0.1 x 10^-6) = 1 x 10^-3

The RC time constant is 1 x 10^-3 or 1 millisecond. Now calculate the time required for this RC circuit to go from 5V to 1.4V (as in Circuit A):

Time = -1 x 10^-3 x ( ln(5.0v ÷ 1.4v) ) = 1.273 x 10^-3

Using SX/B the unit of time is 2 µs, that time (1.273 x 10^-3) works out to about 635 units -- which exceeds the default resolution of RCTIME. What we can do is divide by 635 by 255 (byte value limit) to determine the smallest Resolution required to support the RC combination. In this case it works out to 2.49, so setting Resolution to 3 will allow us to measure the RC network with the greatest accuracy; in this case our measurement units will now be six microseconds (2 x 3). Note that setting Resolution too low will result in RCTIME returning zero.

Another handy rule of thumb can help you calculate how long to charge/discharge the capacitor before RCTIME. In the example above that's the purpose of the HIGH and PAUSE commands. A given RC charges or discharges 98 percent of the way in five time constants (5 x R x C). In Circuits A and B, the charge/discharge current passes through the 220 Ω series resistor and the capacitor. So if the capacitor were 0.1 µF, the minimum charge/discharge time should be:

Charge time = 5 x 220 x (0.1 x 10^-6) = 110 x 10^-6

So it takes only 110 µs for the capacitor to charge/discharge, meaning that the 250 microsecond charge/discharge time of the example is plenty.

A final note about the circuits above: You may be wondering why the 220 Ω resistor is necessary at all. Consider what would happen if resistor R was a potentiometer, and were adjusted to 0 Ω. When the I/O pin went high to discharge the capacitor, it would see a short direct to ground. The 220 Ω series resistor would limit the short circuit current to 5V ÷ 220 Ω = 23 mA and protect the SX IO pin from damage. (Actual current would be quite a bit less due to internal resistance of the pin's output driver, but you get the idea).